Data Protection as a Public Good

Data protection should be subsidised. Here's why.

Background

In contemporary economics, a good is classified as a public good if it is non-rivalrous and non-excludable. Put simply, a good is non-rivalrous if its consumption by one person does not prevent its consumption by another person. A good is called non-excludable if its consumption cannot be prevented by any person once it exists.

Examples of public goods include lighthouses, traffic lights, a functioning judiciary system, open source technology, public ideas, sanitation etc.

Strictly speaking, data protection itself is not a public good because although it is not rivalrous it is excludable. Preventing users from entering the shielded pool is trivial (hypothetically, Namada is of course permissionless). However, it nonetheless exhibits a property commonly associated with public goods, namely having positive externalities. This occurs when one person's consumption of the good benefits another person, and this positive externality is indeed non-excludable. More concretely, when one user enters the shielded pool, it increases the total data protection guarantees for everyone within the shielded pool already, and it is impossible to exclude anyone already in the shielded pool from benefiting from it.

Data Protection's Positive Externality

The positive externality can be explained with a toy example (and accompanying diagram).

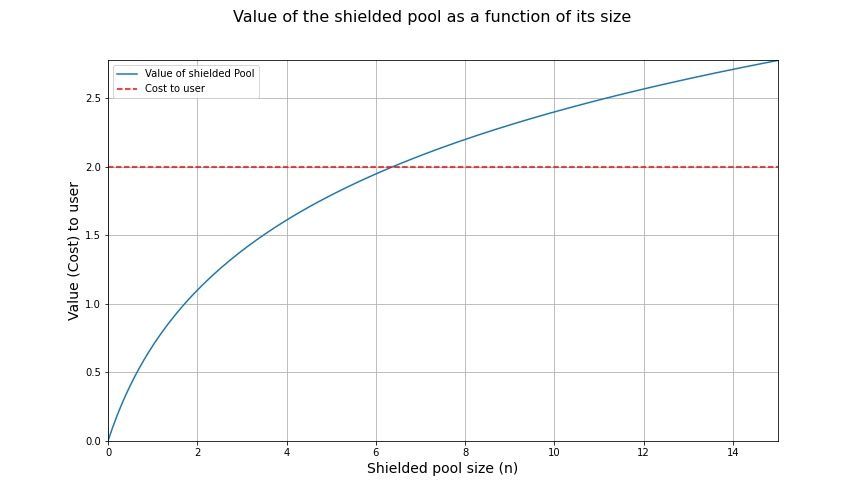
For the sake of simplicity, assume each "agent" in the economy is identical in terms of their preferences. We assume that the user values the opportunity to exist in a shielded set, and that the value of the shielded set increases as the shielded set grows in size. Trivially, a shielded set of 0 people is worth nothing. Further, we assume that each additional increase in the size of the shielded set has a "decreasing marginal benefit" property, in the sense that each additional user contributes less to the overall data protection guarantees as a whole. As the shielded set grows infinitely large, the additional benefit of having someone enter the set becomes negligible. In economics, we tend to represent this through a "utility" function, that simply exists in order to measure cost and value for the agent. A natural choice for a utility function that exhibits the above properties is given by $$ U(n) = \ln (n) $$ where $n$ is the size of the shielded set. Although this is discrete, for simplicity, we will work in the continuous domain.

Additionally, we assume that there exists some unavoidable "cost" $c$ to the user for entering the shielded set. In the real world, this can correspond to learning about zero-knowledge cryptography, handling private keys, and other forms of "effort" and risks that the user may take along the journey. As Gavin Birch points out, there is also the opportunity cost of not lending the asset or staking the asset in a transparent system. Hopefully one day we can figure out how to do this within a shielded set as well.

A visual of the cost-benefit trade-off of the shielded pool

The societal cost

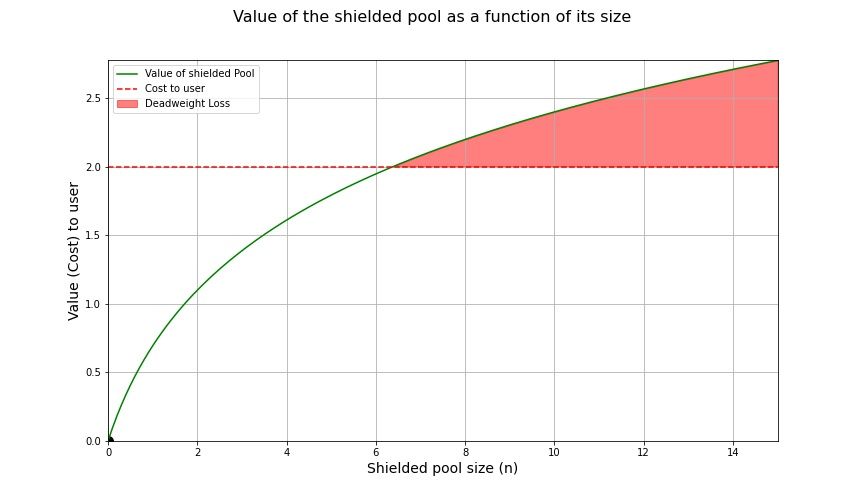
Because of the positive externality associated with entering the shielded set, there is "unrealised value" that is lost in the economy if users are unable to coordinate. Whilst no other user is in the shielded set, the value of the shielded set is 0. In contemporary economics, this "cumulative lost value" (summed over all users in the economy) is referred to as Deadweight Loss. The Deadweight Loss is visualised below by the shaded area between the value and the individual's cost to entering.

A visual of the Deadweight Loss of the shielded pool not existing

Therefore, if the protocol can incentivise a number of users (with ample sizes of assets) to enter the shielded set such that there is sufficient value in remaining in the shielded set, the coordination problem is solved. If the "social planner" was in full knowledge of exactly the amount of users needed in order to achieve this "tipping-point" value $n^\star$ , she could offer exactly the correct amount of subsidy to incentivise the first $n^\star$ users to use the protocol and nothing more.

Correcting the externality

We suggest an alternative approach, whereby we can claim that:

If the subsidy $s(n)$ is inversely proportional to the size of the shielded pool, i.e $s(n) \propto \frac{1}{n}$, then for a sufficiently large constant of proportionality $k$, the subsidy will incentivise the correct number of users to join the system. Additionally, this incentive scheme comes with the added benefit of being finite and predictable. This is not the only possible solution, but is one of them and seems natural.

Example 1: An insufficient subsidy

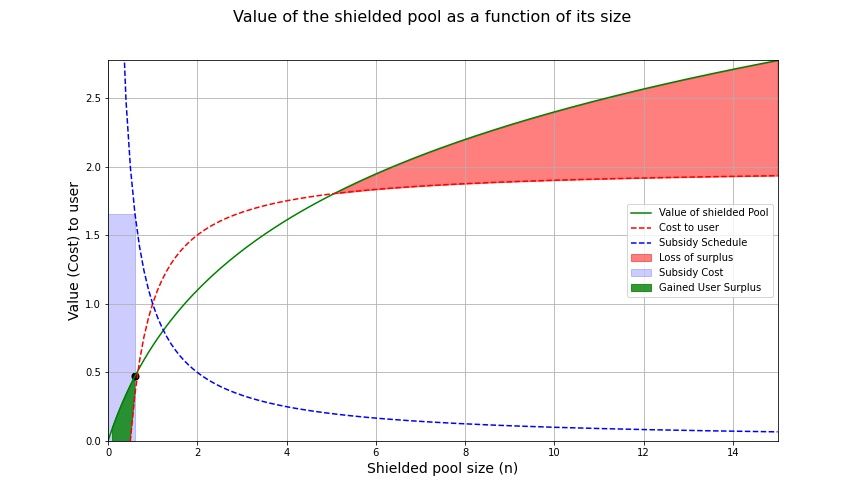
The above subsidy is not sufficient in incentivising users to join the network, although it does lower the threshold slightly. In the above example, the size of the shielded set would increase from 0 to ~0.6. In order to reach the critical mass, we need to incentivise for a shielded set of at least size $n \approx 5.4$

Example 2: A sufficient subsidy

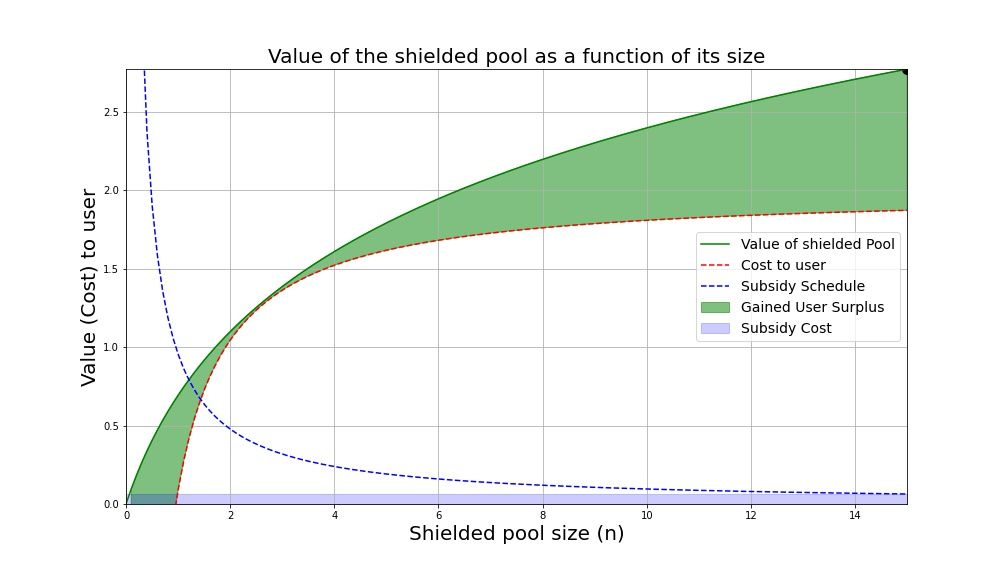
If we increase the incentive to be exactly proportional to the cost for the user, it suffices. An additional nice property with designing the subsidy in this way is that the subsidy becomes easily interpretable; the total subsidy is exactly the cost to any single user, distributed across all users.

A visual of the subsidy when $k = c$

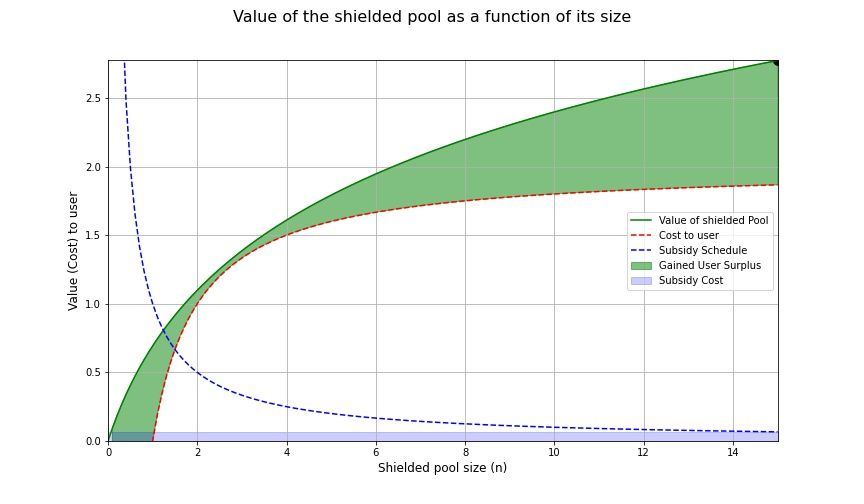
Now the point minimising the areas between the curves is given by the point at which the cost to the user (after the subsidy is taken into account) is tangential to the value of the shielded pool. Challenge: Derive this!

Hint: think about minimising areas and derivative of an integral being the curve itself ...

Example 3: Optimal Subsidy

Which leads us to:

$$\frac{\partial}{\partial x} \ln(x+1) = -\frac{\partial}{\partial x}\frac{k}{x} \Leftrightarrow x^2 -kx - k = 0$$

We also need to ensure that the two curves having exactly one intersecting point. I.e

$$\ln(x+1) = c - \frac{k}{x}$$

These two simultaneous equations can be solved for $k^*$.

The optimal $k^*$ is solved numerically and shown below

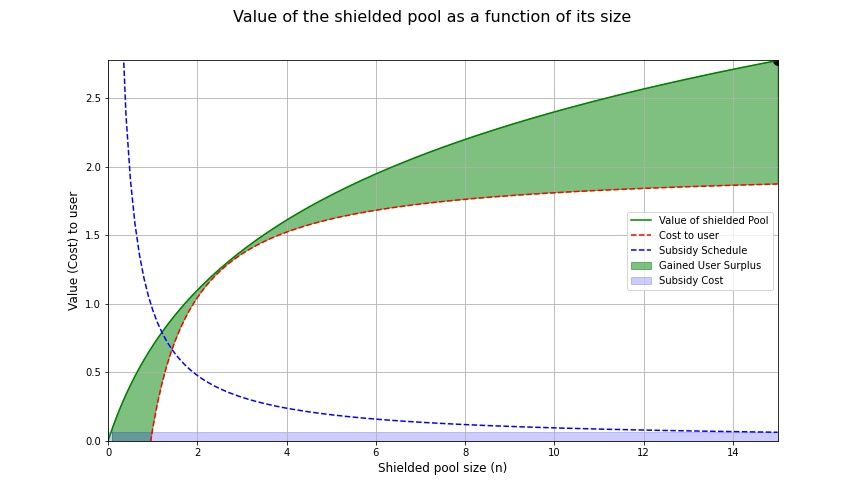
This minimises the cost of the subsidy, at the cost of losing some neat interpretation :)

Conclusion

The key take-away from this article is that entering the shielded set has positive externalities. Without a subsidy, there exists a recursive coordination problem. Users would like to enter a sufficiently large shielded set. However, the shielded set cannot come to fruition because its existence is dependent on assets entering the shielded set to begin with.

With a subsidy, the initial users do not depend on the existence of a sufficiently large shielded set. Instead, the subsidy is programmed to ensure that no matter the size of the shielded set, there is sufficient incentive for assets to enter the shielded set.

Further, with reasonable assumptions, a well constructed subsidy has several nice properties. Its total cost is finite, independent of the size of the shielded set, and fully predictable. Further, it provides unlimited social value (limited only at the total size of all assets in the world). Finally, the solution where $k=c$ is easy enough to implement such that the equation can be understood by a middle school student.

I would like to thank Gavin Birch and stellarmagnet for their insightful comments so far :D