The Multi Asset Shielded Pool and Convert Circuit (MASP & CC) are two key features that Namada offers. The MASP is inspired by the work produced by the Electric Coin Company who developed Zcash, and builds on the Sapling Circuit by implementing multi-asset functionality and programmable asset-conversions.

Background

In this article, I will attempt to explain the MASP at a high level, followed by a slightly more technical explanation (but still doesn't come close to doing it proper justice) in the lower level section. I then ponder about possible applications of the technology that extends beyond what is featured on Namada. This is a long article, and may require two sittings; I would recommend dividing the reading into its parts. Any and all feedback is encouraged and greatly appreciated!

Explain Like I'm 5

At a very high level^[1], the MASP works in the following fashion:

There exists two separate sets of assets:

1. The shielded set
2. The transparent set

From a user's perspective, all transactions in the shielded set are indistinguishable from one another. More specifically, a user is able to see notes being created and nullifiers (objects that make notes unspendable) being revealed, but is unable to make any pairing between nullifiers and notes, nor any pairing between address and note. Further, all notes are indistinguishable in the sense that an observer of a transaction does not see who sent it, who received it, what asset they used to transact, nor how much was sent.

Transparent set

From a user's perspective, all tokens held in the transparent set are equivalent to holding tokens in any other transparent ecosystem. The functionality available to users are transferring assets from one address to another address, as well as bridging assets through the bridges deployed on Namada.

Shielded set

Shielding assets

Assets are minted into the shielded set from a valid zero knowledge proof that produces a "note". The zero knowledge proof is meant to prove a set of things:

1. The asset type in which the note will be denominated ^[2]
2. The amount of the asset
3. The address which owns the note

The underlying asset is sent to escrow.

Transferring Assets

Shielded-to-shielded transfers are constructed through Zero Knowledge Proofs. These proofs ascertain that:

• The notes being spent have not yet been spent
• The notes being spent were previously created
• The user spending the note actually controls them
• The transaction itself preserves balance (no assets created or destroyed)

Further, due to the nature of being Zero Knowledge, these proofs do not reveal any new information about the above claims they set to prove.

Unshielding assets

The user unshielding assets publicly reveals the information used in the minting process, in addition to its nullifier. Once this information is verified, the user is able to take ownership of the equivalent asset, which is released from escrow by a native Validity Predicate. The native VP ensures that the proof is both valid, and that the asset has been converted to its latest epoch ^[3].

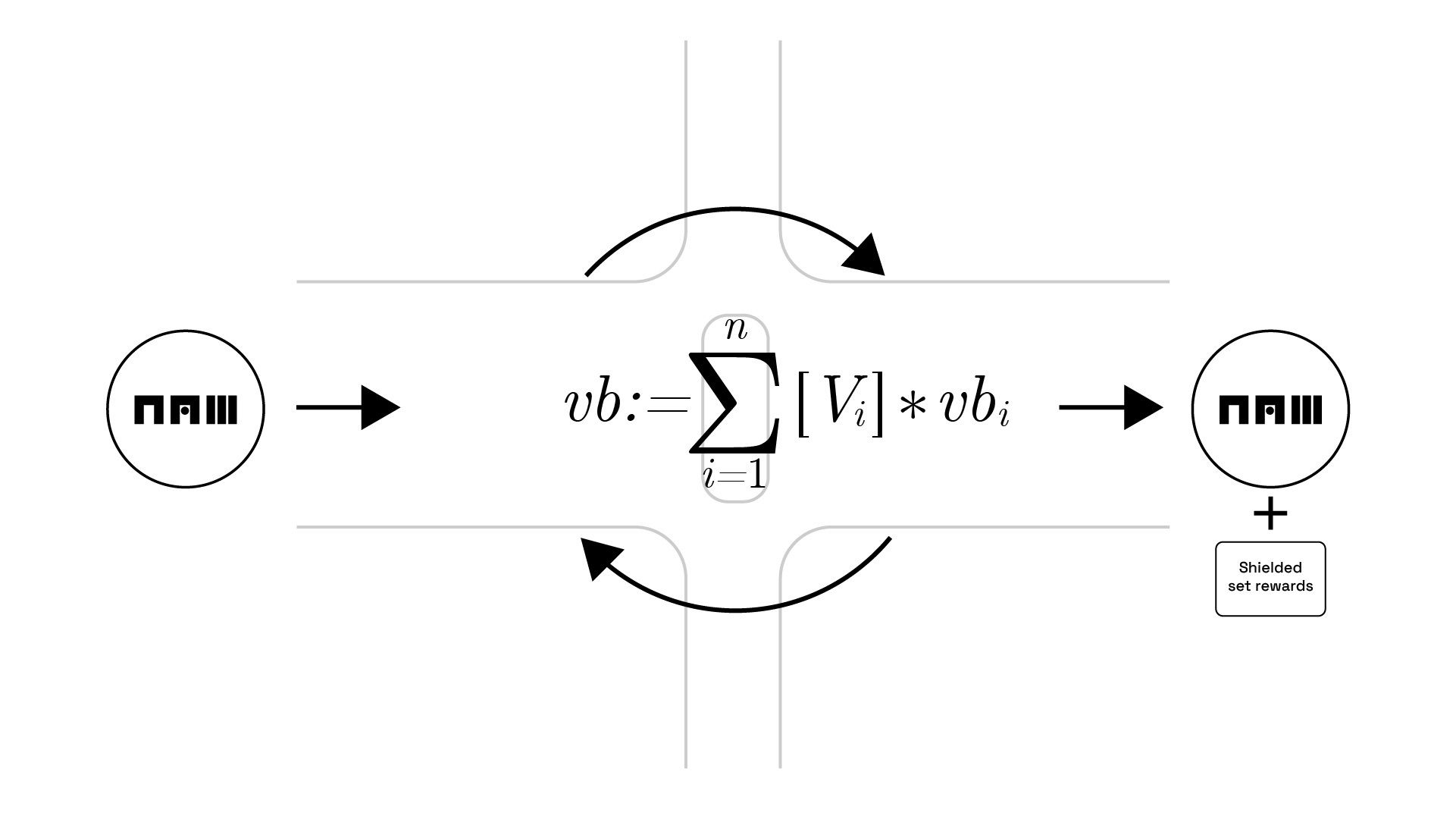
Convert Circuit (CC)

There are two circuits in Namada. The MASP circuit handles the minting and burning of shielded assets (notes). The Convert Circuit (CC) is a separate circuit which works in tandem with the MASP circuit to allow for conversions between assets in the shielded pool which are valid according to a predefined public conversion table.

At a high level, the convert circuit enables assets to be converted without needing to leak privacy through unshielding and or revealing any metadata. Note that these conversions are conversions in the truest sense of the word, and accomplishes the conversion through a mint and burn mechanism, meaning that there is no need for a liquidity pool or counterparty at all, since conversions are exactly that, conversions, not swaps. This is an important feat, as it is essential for making sense of any unified shielded pool. Granted, without the convert circuit, the MASP gives the benefit of a unified shielded set, which is important for assets with low trading volume, but the addition of a convert circuit extends the reach of privacy to much greater functionality (discussed in the applications section).

In Namada, the convert circuit exists in order to provide rewards for shielded assets that are maintained in the shielded pool. The rewards act as a subsidy for reasons of correcting positive externalities. The correction of positive externalities is discussed elsewhere more in detail, both in writing and video.

This is achieved through the following idea:

1. Each asset is attached to an epoch
2. Assets may be converted across epochs
3. The conversion factor is 1-to-(1 + additional subsidy NAM tokens)

Pretty neat huh? I provide a concrete example below, but otherwise I recommend this video, these specs, as well as my attempt at a summary below in the "lower level" section.

1. Alice shields $100 \text{ } NAM_{\text{epoch}_1}$ tokens in epoch 1

• Alice is aware of the CC conversion table publicly available that gives her 1 NAM per 100 NAM she holds in the shielded set per epoch

1. In epoch 2, Alice makes a shielded transfer through the convert circuit, which gives her $100 \text{ } NAM_{\text{epoch}_2}$ plus an additional $1 \text{ } NAM_{\text{epoch}_2}$  
   For a total of $101 \text{ } NAM_{\text{epoch}_2}$

The above conversion table is used in order to calculate the relevant NAM tokens that are distributed as part of Namada's subsidy for holding assets in the privacy set.

At a lower level

Construction of the zk-SNARKs

In order to understand how any shielded transfer is made, it is important to understand how the zero knowledge SNARKs (Succinct Non-interactive Argument of Knowledge) are constructed in Namada. This is because the validity of each shielded transfer is essentially shown by its own zero knowledge argument.

To start with, each zk-SNARK requires "public parameters" that are generated from a "trusted function". This trusted function takes a security parameter $\lambda$ as input, and produces public parameters $pp$ and toxic waste $\tau$ as output.

$$f_{trusted}(\lambda ) = (pp_{\lambda}, \tau)$$

where

1. There exists a proving algorithm that inputs the private details of a shielded transfer and outputs an argument $\pi$ that the transfer is valid
2. There exists a verifying algorithm that inputs the public details of a shielded transfer and an argument $\pi$, and outputs 1 if and only if a proving algorithm generated $\pi$ from the corresponding private details of that transfer (under cryptographic assumptions)
3. There exists a simulator algorithm that on input $pp_\lambda$ and $\tau$ and public details of a "fake" shielded transfer, can produce a "fake" argument $\pi$ for that shielded transfer without knowledge of corresponding private details.

By trusted, we mean that when the function $f_{trusted}(\lambda)$ is evaluated, only the public parameters $pp_\lambda$ are kept and the toxic waste $\tau$ is destroyed and is non-recoverable.

The existence of $\tau$ is used to show that the argument $\pi$ is zero-knowledge and the verifying algorithm learns nothing from $\pi$ other than its validity.

Note commitments

Note commitments are defined by homomorphic pedersen commitments. Homomorphic pedersen commitments are created through two generators: the value base and the randomness base.

In order to encompass multiple assets, Namada employs a dynamic generator that derives a new value base for each asset. Further, this dynamic generator uses pseudo-randomness to ensure that it is computationally infeasible to find the relationship between asset types.

From the paper:

The asset generator (also known as the value base) is a valid ctEdwards curve point on the Jubjub curve, whose compressed bit representation is the BLAKE2s image of the asset identifier

The Blake2s preimage of the asset generator defines the asset identifier.

In Sapling, a necessary security assumption in order to avoid the ability for attackers to open value commitments improperly (and hence spending notes they do not "own") is that there can not exist any discrete log relationship between the base point (asset generator) and the randomness parameter (a.k.a trapdoor). The addition of multiple asset types places an additional assumption on the setup of the circuit, in that there can also not be any discrete log relationship between assets' generator base points. This would allow users to open value commitments across assets improperly.

A more technically involved, yet still important assumption is that there should not exist two asset generators that can negate each other, as would occur if the curve points were the P and [-1]P. This can be avoided using proper precautions as well.

The Convert Circuit

At a lower level, the convert circuit works by a conversion table and a synthetic asset that has a tupled structure.

More specifically, a valid predefined conversion is a list $[(A_1, V_1), (A_2, V_2), ... (A_i, V_i), ... (A_n, V_n)]$ of tuples $(A_i, V_i)$ of Asset $i$ and signed integer $V_i$ that define a new asset generator $vb_{cc}$ given by

$$vb := \sum_{i=1}^n [V_i]*vb_{i}$$

Where $vb_i$ is the corresponding asset generator of $A_i$. This may seem confusing at first, but if we think of it in its simplest form, we can define the conversion of
$$vb_{\textit{NAM_INF}} := vb_{\textit{NAM_EPOCH}_{i}} \text{ }- vb_{\textit{NAM_EPOCH}_{i-1}} \text{ }+ [\text{rewards factor}]vb_{\textit{NAM_EPOCH}_{i}} $$ to mean a circuit that allows you to convert one NAM token from the previous epoch to the current epoch, that also gives you additional NAM tokens in reward. This exists in order to incentivise users to keep their assests in the shielded set, in an effort to subsidise the shielded set.

Applications

There are many different applications for this type of technology outside of the realm of providing inflationary subsidies. Below, I list my thoughts for potential ideas.

Shielded taxation

Assume we are in a world where blockchains are mainstream and the government have finally been able to monitor and implement a taxation scheme on the transparent side of things. This is not difficult to do given that now all data is public. People should no longer need to submit tax returns because it should just be an automatic calculation. However, at the same time, the government is monitoring every transaction. People might want to turn to a more privacy-enabling solution (and rightly so).

With a custom CC, the government would be able to implement a wealth/income tax even within a shielded set.

The conversion table could look something like:

Taxation at rate $tax$
$$[-1] \text{ } NAM_{epoch_i} \text{ }  [+ (1-tax)] \text{ } NAM_{epoch_{(i+1)}} $$

An income tax would require more thought and deliberation but is still possible.

How would the government enforce this transaction over a shielded set?
The government would be able to enforce this by making sure that all unshielding requires the latest denominated epoch of each asset.

Hence, taxation is achieved without affecting any privacy guarantees. In order to "collect" these taxes, the government would simply be allowed to mint an equivalent value of assets that have been burnt thus far by the above convert circuit.

In addition to its use case as a funding mechanism for the government, this type of convert circuit can be used as an incentive mechanism (stick instead of carrot) for shielded transfers. For example, assets denominated in epochs older than a certain date can become taxed when converted, incentivising more frequent conversions.

Crowdfunding and voting

Similar to the lending and borrowing mechanism, the convert circuit can be used to mint assets that correspond to a "promise" on claims, and do so completely privately.

For example allow the conversion of 1 "Vote token" $\rightarrow$ 1 "Voted token" if the user interacts with a contract/VP that handles voting on a proposal.
Then, once the voting period is over, close the conversion and allow the for the reverse conversion (or something more involved). This could similarly be used for crowdfunding, where the reverse conversion is opened if the funding was not met at the deadline and otherwise not opened.

Conversion Circuit:

During voting / funding period
$$[-1] \text{ Vote/funding token } [+1] \text{ Voted_for_x/funded_project_x token }$$
After voting/funding deadline
$$[-1] \text{ Voted_for_x/funded_project_x token } [+1] \text{ Voting/funding token }$$

Shielded prediction markets

This would obviously require some form of trusted oracle, but the idea would be that conversions could be used to allow for shielded trustless prediction markets.

I will use the Super Bowl LVII as an example because it is relevant during the time of writing. Let's say we wanted to make a prediction market on whether the Philadelphia Eagles will win the Super Bowl this year. This will be a binary outcome, and the prediction market will be constructed such that $YES$ tokens are converted to 100 NAM if the Eagles do indeed win the Super Bowl, and otherwise $NO$ tokens will be able to be converted to 100 NAM tokens if they don't win.

A custom validity predicate would handle adding new conversions into the conversion table that it will then close/open depending on the oracle price.

The new conversion in the conversion circuit will allow users to deposit 100 NAM tokens for both a $YES$ and a $NO$ token.

Users can then trade these tokens on the market, and do so privately. This would require users to discover counterparties, and is easily done with opposing views off-chain. For on-chain counterparty discovery, this can either be baked into the protocol (on future Anoma blockchains), through integration with well-established swap-enabling markets (e.g Osmosis) or through a trust-minimal frontend that allow users to trade some privacy and trustlessness for counterparty discovery and an escrow.

How would this work more concretely?

For example, if I think the Eagles will with exactly $x%$ probability, then I should be willing to buy YES tokens for a at any price $p$ such that $p<x$ (assuming I don't mind risk 👀). Equivalently, I should be willing to buy NO tokens at any price $p<100-x$. Further, I would like to sell these respective tokens with the inequality sign flipped. This creates a market where people can interact and make credible commitments to their beliefs. Once the result has been decided, the conversion is opened and participants can convert their tokens. Assume the Eagles do win, then people who bought YES tokens in exchange for NO tokens at any price less than 100 NAM will be able to profit.

Although there are benefits to doing this publicly on a transparent blockchain, as Vitalik Buterin explains , there are benefits for having this private as well. Perhaps you don't want to show your Philadelphia born friends (i.e Brent Stone) that you bet against their team winning the Super Bowl ...

Conversion Circuit:

Before uncertain outcome
$$[-100] \text{ NAM } [+1] \text{ YES_EAG } [+1] \text{ NO_EAG } $$
After outcome becomes certain
If SuperBowl.winner == 'Eagles':
$$[+100] \text{ NAM } [-1] \text{ YES_EAG }$$
else:
$$[+100] \text{ NAM } [-1] \text{ NO_EAG } $$

NFT upgrades

Programmable Non Fungible Tokens would also be possible within the shielded set. An example of this would be a PokéNAM that wants to evolve in private. Luckily this would be completely possible if the correct convert circuit exists. Something like

$[-1] \text{ CharNAMder} \text{ } [-81000]\text{ EXP} \text{ } [+ 1] [\text{CharNAMeon}]$

Imagination is really the limiting factor here.

Shielded borrowing/lending protocol

This idea requires a bit of imagination and is not directly possible with just a convert circuit, but with extra logic is not entirely infeasible.

The most straightforward example is to allow anonymous lending with pseudo-anonymous borrowing. This is possible because tokenised lending is directly fungible, but because of collateral requirements, tokenised borrowing is not.

I'll use lending ETH as an example. One possible (and perhaps naive) way of achieving this is by creating the conversions

1. $$[-1]NAM \text{ } [+1] \textit{Lent_}NAM$$
2. $$[+1]NAM \text{ } [-1]\textit{Lent_NAM} \text{ } [-i_{\text{epoch}}* (\Delta \text{EPOCH]})NAM$$

• Where $i_{\text{epoch}}$ is the per-epoch interest rate.
• $\Delta EPOCH$ is the epoch difference

Then a VP would handle (with transparent addresses) a contract that allows the borrowing user to borrow NAM in a collateralised fashion. In this way, if a borrower reaches the liquidisation threshold (ideally over 100% collateralisation), liquidation can happen in a decentralised way that is incentivised by arbitrage. In other words, one could use the bog-standard decentralised borrowing setup we have today in apps like AAVE.

In order to also allow shielded borrowing, further imagination is required. Now we need a way to make collaterisations pooled without transferring too much risk onto lenders or across borrowers. An implementation would need to be very weary of the lemons effect evolving from this information asymmetry.

The first two additional conversion rates are straightforward:

1. $$[-1]ETH \text{ } [+1]\textit{Borrowed_}NAM \text{ } [+1]\textit{Lent_}ETH$$
2. $$[+1]ETH \text{ } [-1]\textit{Borrowed_}NAM \text{ }
   [-i_{\textit{epoch}}* ( \Delta \text{EPOCH})]NAM \text{ }
   [-1]\textit{Lent_}ETH$$

However, we now have two additional difficult problems to handle. What incentives exist for borrowers to pay their interest? What incentivises borrowers to ensure their collateralisation thresholds are met? How do we reconcile the difference between borrowed NAM, and NAM, since these assets are no longer fungible.

A proposed solution is to incentivise "reconversion" of NAM by paying off "collateral debt" periodically. This would add a couple of new conversion rates:

$$[+1]\textit{Borrowed_NAM}_{\textit{epoch}_T} \text{ }  [-1]\textit{Borrowed_NAM}_{\textit{epoch}_{T-j}} \text{ ...} $$

$$  \text{...  } [+r_{j}] ETH \text{ } [-i_{epoch}*( \Delta \text{EPOCH})]NAM$$

• Where you can convert borrowed NAM from some old epoch to a current epoch's denominated NAM, if you supply the correct amount of additional collateral, plus interest. The implementation of this would perhaps be difficult and would require a new conversion each epoch in order to minimise risk. The idea would be that only the most recent denominated borrowed NAM would be accepted as payment, and there would be risk attached to it. In this way, the borrowed assets in circulation should always be sufficiently collateralised.
• $$[-1]\textit{Lent_}NAM \text{ } [+\text{min_ETH_per_NAM}]ETH$$
• This is just a conversion that should be used as a last resort for a lender looking to exit.
• $$[+1]ETH \text{ } [-1]\textit{Borrowed_}NAM_{\text{epoch}_T}$$
• Then borrowed NAM can be converted back into its collateral, since all debts will be paid through conversion 1.

Dealing with liquidations is definitely the most difficult part about getting this to work, since you want collateral placements to be anonymous.

With a non-dynamic convert circuit, this would have to be done with fixed interest rates. However, with dynamically programmable convert circuits (see https://github.com/anoma/taiga 👀) it should be possible to incorporate dynamic supply and demand to handle this in a more economically efficient manner.

Conclusion

In short, there is much more to the technology behind the MASP than the name suggests. Coupled with the convert circuit, the technology becomes particularly powerful and allows for a large number of potential applications. At Namada, we are focused on providing a secure shielded payment system (at the moment), but we hope that some readers will pick up the ideas behind the convert circuit to implement and invent new cool ideas that can really push the forefront of ZK applications.

Footnotes

[1]: For more details, see Sasson, Eli Ben, et al. "Zerocash: Decentralized anonymous payments from bitcoin." 2014 IEEE symposium on security and privacy. IEEE, 2014.

[2]: The asset type is more general than what one might expect. The asset type on Namada can be used to denote an epoched asset as well (e.g $NAM_\text{epoch_42}$). Epoched assets play a role in the convert circuit.

[3]: See the relevant section for more information on the Convert Circuit